Оригинал статьи: http://www.ttr.com/TELSIKS2001-MASTER-1.pdf

Перевод в формате MS Word: http://halerman.narod.ru/Tesla/Voltage_Magnification.doc

 

"Калькулятор катушки Тесла со стоячими волнами": http://hamwaves.com/antennas/inductance.html

Доработка калькулятора в формате VBA Excel: Калькулятор высокочастотных катушек

 

ВЫСОКОЧАСТОТНЫЕ КАТУШКИ, ВИНТОВЫЕ РЕЗОНАТОРЫ И  УВЕЛИЧЕНИЕ НАПРЯЖЕНИЯ ИЗ-ЗА КОГЕРЕНТНЫХ ПРОСТРАНСТВЕННЫХ МОД

 

K.L. Corum,

CPG, Inc., Plymouth, NH, USA

J.F. Corum,

Institute for Software Research, Inc., Fairmont, WV USA

“Is there, I ask, can there be, a more interesting study than that of alternating currents.”

Nikola Tesla, (Life Fellow, and 1892 Vice President of the AIEE) ¹

 

Аннотация - Чтобы смоделировать проволочную катушку, как анизотропно проводящий цилиндрический объем, можно применить уравнения Максвелла и описать резонансное поведение спиральной структуры. Так можно получить не только коэффициент распространения и волновое сопротивление для такого волновода со спиральной поверхностью, но и также его резонансные частоты, «собственную емкость», и коэффициент умножения напряжения от стоячих волн. Кроме того, катушку Тесла можно свести к обычной сосредоточенной индуктивности, с укороченной электрической длиной.

 

I. Введение

 

Одной из наиболее значительных проблем в науке об электричестве, является описание проводника, уложенного в компактном объеме, и определения электрических свойств результирующей структуры. Задача интересна не только для очень низких частот, где такая композиция может рассматриваться как сосредоточенный элемент (катушка индуктивности), но и для таких частот, где распределение тока по структуре не является однородным, и классическая модель из сосредоточенных элементов не состоятельна. Геометрия простой катушки со спиральной намоткой является предметом изучения этой статьи.  (Это общее заблуждение, что полевой анализ необходим только при относительно высоких частотах. На самом деле, такой подход необходим всякий раз, когда распределение тока по структуре не является однородным.) Adler, Chu и Fano указали, на три важных черты линейных систем с высокой добротностью:

(1) их свободные колебания слабо затухают;

(2) их входное сопротивление имеет резкое и быстрое изменение в окрестностях резонанса;

(3) их полевое распределения имеет характерное пространственную структуру, что сопровождается резкой селективностью поведения всей системы. Именно об этой третьей особенности часто «…забывают  в анализе сосредоточенных сетей, но имеющей огромное значение для понимания распределенных резонансных систем.»² Спирально намотанная катушка Тесла является именно такой системой, как будет показано ниже в статье. (Анализ выполняется для линейной системы – до возникновения разряда, когда и возникает феномен роста напряжения. При разряде система имеет нелинейное поведение, конечно.)

 

II. Цилиндрическая спираль

 

A. Формулирование задачи

 

Равномерная цилиндрическая спираль описывается ее радиусом (r = a), ее шагом (или межвитковым расстоянием “s”), и ее углом наклона витка ψ, т.е. углом между плоскостью витка с плоскостью, перпендикулярной к оси структуры (z). Геометрически, ψ = cot^-1(2πa/s).

Волновое уравнение не разделяется в спиральных координатах, и не существует строгого решения уравнений Максвелла для цилиндрической спирали.³

Однако, для высоких частот проволочную спираль с большим количеством витков, приходящимися на длину волны в свободном пространстве (например, катушка Тесла), можно представить идеальной анизотропно проводящей цилиндрической поверхностью, которая проводит только в винтовом направлении. Проводимость по нормали к винтовой линии принимается равной нулю. (Эта цилиндрическая трубообразная структура является классической моделью спиральной поверхности Ollendorf.⁴)

Формально, для гармонических полей (предположим, с зависимостью e^jωt от времени), однородные векторные уравнения Гельмгольца

 

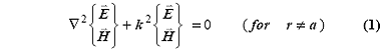
где k = ω(με)^1/2 = 2π/λ = k_o(ε_rμ_r), должны быть решены с соответствующими граничными условиями. [Переход от квазистатической теории поля к классической сосредоточенной модели, происходит при бесконечной длине волны (или, иначе, как c®¥).] Уравнения Гельмгольца разделяются на одиннадцать уравнений в трехмерной ортогональной системе координат, так что можно получить решение. В спиральной системе координат так не получится сделать. Спиральная структура поддерживает распространение вдоль продольной оси (z) бегущей волны с зависимостью в форме e^{j(ωt - βz)}, где b должен быть определен. (Мы временно пренебрегаем диссипацией, так что фактор распространения g =a + jb® jb.) Поля можно разложить на поперечные и продольные компоненты, поэтому есть оба вида TE и ТМ мод вдоль этого анизотропного волновода . Кроме того, оператор Ñ  разделяется на поперечный и продольный операторы, то есть

Ñ = Ñ_t (jb) ż, дает оператор Лапласа Ѳ = Ñ_t² - b², и так что оператор Даламбера [Ѳ + k² ] = [Ñ_t² + (k² - b²)], и уравнение (1) разделяется на уравнение:

 

 

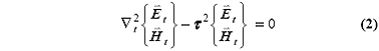
для поперечных компонент поля, и уравнение

 

 

для продольных компонент поля. В этих выражениях, важнейшее радиальное волновое число τ, дается

 

 

Центральным вопросом для распространения волн в спиральных структурах, является поведение τ, в зависимости от частоты и геометрии спирали (a, s и ψ). В отличие от волновода с TEM-модами, и это важно, E_z ≠ 0 и H_z ≠ 0 в спиральном волноводе. Более того, b ≠ k (где k² = ω²με , представляет собой постоянную распространения для плоской волны).

Из цилиндрической симметрии, осевая составляющая внутренних (i) и внешних (o) гармонических полей будет суперпозицией, распространяющихся вперед колебаний в виде набора радиальных, азимутальных и осевых функций в виде

 

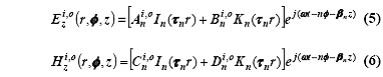
где восемь констант A, B, C, D [внутри (индекс i) и снаружи (индекс o) спирали] должны быть определены для каждой моды из граничных условий и источника сигнала, а β_n является постоянной распространения вдоль спирали для n-ой моды. В системе реально присутствует также суперпозиция линейно сложенных обратно распространяющихся мод, но на данный момент, мы будем рассматривать только распространяющиеся вперед моды. Радиальные функции I_n(x)) и K_n(x) являются модифицированными функциями Бесселя первого и второго рода, соответственно, n-порядка и аргумента x. При наличии азимутальной круговой симметрии вокруг соленоида, мы имеем только моду с  n = 0.^5,6 (Она была названа T_o модой спирального волновода.⁷)

 

B. Физические ограничения

 

Для того чтобы найти другие компоненты поля внутри и вне спирали, можно применить закон Ампера и закон Фарадея, для того чтобы выразить E_r, E_φ, H_r, и H_φ через производные E_z и H_z. Рассмотрим n = 0 моду (азимутальная симметрия в полях). Физически, значения полей должны быть конечной величиной при r=0 и стремиться к нулю при  r®¥. Из свойств модифицированных функций Бесселя, это означает, что A^o, Bⁱ, C^o, Dⁱ тоже должны стремиться к нулю. Используя соотношения для производных модифицированных функций Бесселя,

 

а также тот факт, что K₀(τr) расходится при r®0, можно найти выражения для полей внутри спирали (r £ a). Вне спирали  (r ³ a), I₀(τr) расходится при r®¥, и выражения для внешних полей легко определяются. Однако, полученные решения будут содержать неизвестные константы A^o, Bⁱ, C^o, Dⁱ и постоянную распространения τ. Эти константы и постоянную распространения можно будет определить путем наложения анизотропных граничных условий по винтовой поверхности при r = a.

 

C. Граничные условия винтовой поверхности

 

Существует три граничных условия на анизотропной винтовой поверхности, которые следует взять в расчет. Их можно суммировать следующим образом:

(1) граничные условия Максвелла для цилиндрической поверхности позволяют приравнять нулю внутренние и внешние компоненты напряженности поля вдоль (т.е. параллельно) провода при r®a:   E(a) =0. Это можно записать в виде

 

 

(2) условие непрерывности для нормальных (т.е. перпендикулярных) проводу компонент напряженности электрического поля, по всей цилиндрической границе, при пересечении ее:

 

 

(3) условие непрерывности для продольных (параллельных) проводу компонент напряженности магнитного поля, по всей цилиндрической границе, при пересечении ее:

 

 

Накладывая эти граничные условия на выражения для внутренних и внешних полей, получим четыре уравнения для четырех оставшихся неизвестных констант Aⁱ, B^o, Cⁱ, D^o, и постоянной распространения τ.

 

 

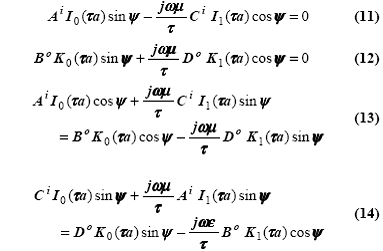
Это четыре линейных уравнения с пятью неизвестными, и решение можно найти либо прямой алгебраической подстановкой, или методом определителей.

 

D. Распределения поля и распространяющиеся моды

 

Совместное решение первых трех уравнений (для n = 0 случай) позволяет выразить все константы (B^o, Cⁱ, D^o) через A₀ⁱ. Используя эти константы и решения для поля, полученные для (r £ a) и (r ³ a) в пункте B, получим уравнения для внутренних и внешних полей винтовой структуры, выраженных через Aⁱ (которую можно напрямую связать с ЭДС). В результате получается следующий набор прямо распространяющихся ТЕ и ТМ мод.

 

 

 

 

 

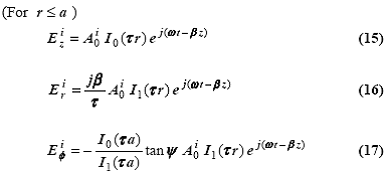
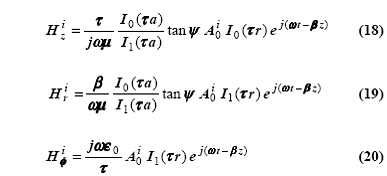
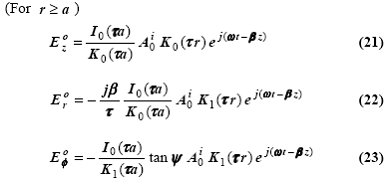
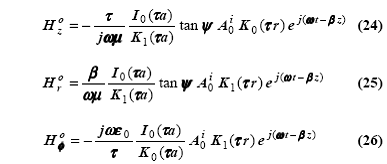
Хотя решения, на первый взгляд, могут показаться сложными, этот набор выражений является чрезвычайно полезным инструментом для определения свойств как сосредоточенных, так и распределенных высокочастотных катушек. Асимптоматика K_n(τr) является экспоненциальной, что означает, что поля спиральной катушки это поверхностные волны, распространяющиеся по спиральному волноводу.⁸ Кстати, также следует отметить, что как внутри, так и снаружи катушки, отношение продольной компоненты поля к азимутальной, определяется выражением:

 

 

Таким образом, это отношение определяется отношением длины окружности к шагу спирали, E_z » E_φ. Это соотношение полей является одним из основных геометрических свойств катушки, что еще давно утверждали Contaxes и Hatch, исходя из уравнений Максвелла.⁹ (В своих аргументах они основывались на формулы для индуктивности, которые предполагают, что скорость распространения бесконечна, то есть - нет никаких стоячих волн в катушках.) Такие же результаты были получены в квазистатическом приближении Fano, Chu и Adler.¹⁰ Можно графически изобразить уравнения (15) - (26) для распространяющихся волн, чтобы показать, структуру поля в катушке. ^11,12 Напомним, что на данный момент, длина спиральной катушки предполагалась бесконечно длинной, так что в решении получились только прямо распространяющиеся бегущие волны. Позже, с введением произвольного сопротивления нагрузки, появятся отраженные волны и, соответственно, возникнет распределение стоячей волны, как и в любой волноводной системе.

 

E. Постоянная распространения

 

Осталось неиспользованным уравнение (14) для анизотропных граничных условий. После совместного решения уравнений (11) - (13) получены константы (B^o, Cⁱ, D^o), выраженные через A₀ⁱ, их можно подставить непосредственно в уравнение (14), чтобы получить уравнение с собственными значениями для τ (см. Калькулятор высокочастотных катушек ):

 

 

Это чрезвычайно важное уравнение, и его нужно решить для τ, при указанной частоте ω, и параметрах спирали “a” и “s” (и угле ψ). Поскольку это уравнение является определителем системы уравнений (11) - (14), его еще называют детерминантным уравнением для τ. Тривиальное множество решений получается, когда τ²=0. Из уравнения (4), следует, что это TEM волны с β = ±k. Однако, для медленных волн, τa >> ka (так как λ_g << λ_o). Следует напомнить, что мы рассматриваем только цилиндрически симметричный (n = 0) случай. На ультравысоких и сверхвысоких частотах, поля больше не будет сохранять свою окружную симметрию и станет интересно изучить моды высшего порядка. Детерминантное уравнение для этих мод можно легко вывести, также оно приведено в литературе. Трансцендентное выражение, приведенное в уравнении (28) легко решается численно для заданной геометрии. Для случая τa ³ 10, который получается, когда длина окружности спирали больше λ₀/4 или на длине волны  не укладывается очень большое число витков (т.е. противоположно случаю обычного волновода бегущей волны), тогда отношение модифицированных функции Бесселя (K₁I₁ / K₀ I₀)®1 и τ » k csc ψ. Фазовая скорость v_p, в этом случае становится

 

 

Одной из самых ранних работ посвященных задаче распространения в спирали, была работа Pocklington¹³ (интегральное уравнение излучения антенны), анализ был проведен для этого режима. Это выражение не столь полезно, когда у катушки большое количество витков, приходящихся на длину волны вдоль оси спирали, или для катушки малого диаметра по сравнению с длиной волны в свободном пространстве (как в случае с катушкой Тесла). В таких случаях лучше всего, это численно решить уравнение (28), для получения постоянной распространения. Для катушек с большим числом витков на длине волны, которые мы и рассматриваем, была найдена полезная инженерная аппроксимация, для основного резонанса. Постоянная распространения может быть выражена в терминах волнового числа k, и коэффициента замедления скорости, V_f = v_p/c = k/β, как

 

 

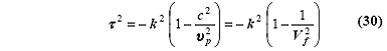
где v_p является фазовой скоростью вдоль оси спирали, а k = w/c = 2p / λ₀. То есть,

 

 

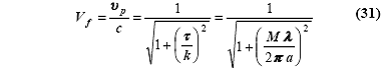
где τ должна быть определена как корень уравнения (28). [Параметр М определяется как M = τa.] Построив левую и правую части уравнения (28) для предполагаемого значения τa и графически определив точку пересечения, можно аппроксимировать выражение для М (Kandoian и Sichak¹⁴⁾, соответствующее четвертьволновому резонансу, и применимо для спиралей с 5ND² / λ₀ £ 1 (где N = 1/s является число витков на единицу длины, и D = 2a диаметр спирали), то есть - для катушек с диаметром значительно меньшим, чем длина волны в свободном пространстве. Kandoian и Sichak обнаружили, что М может быть представлена примерно как M = 20π²D⁵/(sλ)^5/2. Во всех наших публикациях, мы перевыразили это соотношение через коэффициент замедления скорости распространяющейся волны, по простой формуле:

 

 

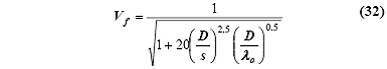
где D = 2a диаметр спирали. Мы обнаружили, что это выражение дает приемлемый результат (ошибка менее 10%) для большинства практических применений, включающих распространение волн в спиральных резонаторах с азимутальной симметрией поля (т. е. для T_o моды). Коэффициент замедления скорости распространения вдоль оси z, представлен на рисунке 1, как функция от D/λ₀, при различных намоточных данных катушек (витков / λ₀). Плотно намотанные катушки являются структурами с медленными волнами. Экспериментально, скорость волны и коэффициент замедления могут быть определены путем измерения распределения узлов и пучностей стоячих волн вдоль оси спиральной структуры, при помощи подвижного зонда.

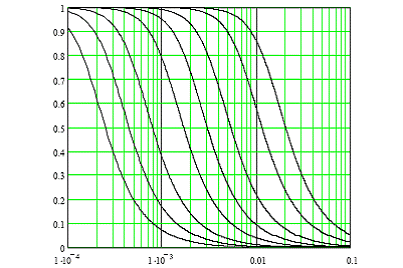
Рисунок 1. Зависимость V_f  от D/λ₀ для катушек с N = 1/s = 10,000; 5,000; 2,500; 1,000; 500; 250; 100; 50 витков/ λ₀, соответственно (слева напрво).

 

F. Волновое сопротивление спирального волновода

 

Существует несколько выражений для спиральных катушек, которые используются в справочной литературе в качестве “импеданса”  (дело в том, что в анизотропной структуре спирального волновода есть ТЕ и ТМ волны). Мы уделим наше внимание “волновому сопротивлению передающей линии”, выражение для которого, получил Sichak много лет назад. Это соотношение является особенно полезным, когда спиральная катушка рассматривается как резонатор, и можно пользоваться диаграммой Смита (Вольперта-Смита) и диаграммами полных сопротивлений.

Это соотношение получается следующим образом. Рассматривая спиральную катушку как простой проводящий волновод, можно определить эквивалентное волновое сопротивление передающей линии в три этапа. Во-первых, как и для коаксиальной линии, используется уравнение (22), и определяется поперечное напряжение в некоторой плоскости z = 0: (Pierce приписывает этот шаг Schelkunoff.¹⁵)

 

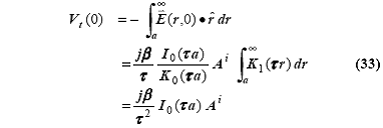
Обратите внимание, что было использовано интегральное соотношение

 

 

Затем, следуя Sichak¹⁶, эффективное волновое сопротивление может быть найдено через отношение поперечного напряжения к току проводимости (определяемому из уравнения полей). Продольный ток проводимости получается, как:

 

 

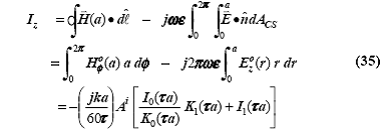
где используется, как равенство ωε = k / Z₀ , так и интегральные соотношения для модифицированных функций Бесселя

 

 

Эффективное “волновое сопротивление” для изолированного винтового волновода определяется (также как и для ТЕМ передающей линии) отношением поперечного напряжения к продольному току проводимости

(Z_c = V_t  /  I_z ), как

 

 

Пользуясь определителем Вронского для функций Бесселя, ¹⁷

 

 

который можно раскрыть, используя известные соотношения для производных функций Бесселя,

 

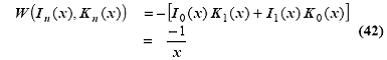
получаем эффективное волновое сопротивление винтового волновода, как

 

 

Этим важным выражением для импеданса удобно пользоваться при работе с диаграммой Смита (Вольперта-Смита) и для инженерных расчетов. Стоит отметить, что для винтовых анизотропных волноводов, эффективное волноводное сопротивление зависит не только от геометрии катушки (как это было бы для TEM коаксиальной линии без потерь и спаренной передающей линии), но и также зависит от частоты возбуждения (см. Калькулятор высокочастотных катушек ).

 

G. Примечания

 

Есть два замечания, которые мы хотели бы здесь сделать. Во-первых, мы отмечаем, что¹⁸

 

 

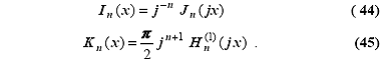
где представлены соотношения между обычными функциями Бесселя n порядка с комплексным аргументом, и функцией Хэнкеля первого рода n порядка с комплексным аргументом. Таким образом, уравнение (43) для волнового сопротивления также может быть записано в виде

 

 

и является тем выражением, которое первоначально получил Sichak. Во-вторых, мы ранее уже использовали уравнение

 

 

как аналитическое выражения для волнового сопротивления винтового волновода возле четвертьволнового резонанса (h =  λ_g / 4). Высота катушки h, и D ее диаметр (обе величины измеряются в одинаковых единицах измерения). Эта формула была фактически получена Schelkunoff как “среднее эффективное волновое сопротивление” в его классической модели передающей линии для биконической антенны. Единственное изменение состоит во включении эффекта медленных волн. Как это соотносится с уравнением (43)? Асимптотические выражения при малых значениях аргумента модифицированных функций Бесселя первого и второго рода  (n = 0)

 

Для медленных волн (b_g  〉〉 k_o) уравнение (30) дает τ ® 2p/ λ_g, и уравнение (43) переходит в уравнение

 

 

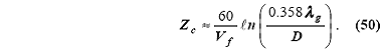
Сравним этот (50) результат с приближенным выражением Schelkunoff для четвертьволнового резонанса

 

 

Так, вблизи резонанса, обе формулы отличаются лишь на несколько процентов, что можно считать успехом предыдущей модели (Sichak).

 

III. МОДЕЛЬ ПЕРЕДАЮЩЕЙ ЛИНИИ

 

Формальный анализ, представленный в разделе II, хотя и таил в себе проблемы, привел к весьма практичной модели для радиоинженера. Выбор геометрических параметров спиральной катушки и частоты возбуждения [по формуле (28)] позволяют определить параметр τ. [как альтернативный вариант, по уравнению (32) геометрические параметры определяют коэффициент замедления скорости V_f, и соответственно τ определяется по формуле (30).] Итак, у нас есть постоянная распространения вдоль оси

 

 

для анизотропных спиральных волноводов. Кроме того, у нас есть его волновое сопротивление. [Фактически, все выкладки в Раздел II нужны были лишь для получения этих двух параметров (Z_c и β_g) для спирали.] Таким образом, входной импеданс и сопротивление нагрузки, для передающей линии с низкими потерями длиной h, в этой модели связаны знакомым уравнением

 

 

“Напряжение” распространяется по линии как интерференционная картина прямых и обратных бегущих пар волн, которые являются решениями волнового уравнения передающей линии и, в данный момент, предполагается, что они являются монохроматическими и когерентными. Распределение напряжения вдоль линии, имеющей потери, определяется известным выражением

 

 

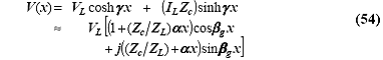
где координата x измеряется с обратным знаком от нагрузки, V_L является напряжением на нагрузке, I_L является током в нагрузке, и α является коэффициентом затухания, а также ряд других параметров, определенных выше. Для случая четвертьволновой линии (β_gh = p / 2) с низкими потерями на излучение, открыто замкнутой на конце (Z_L = ¥), уравнение (54) дает соотношение роста напряжения (или увеличения) между верхом и низом резонатора как^{19,20,21,22,23,24}

 

 

где V(-h)  это напряжение, индуцированной в базе (нижняя часть) структуры. Это резонансный трансформатор Тесла. ^25,26 (Очевидно, что нагрузка может быть емкостным электродом, который будет выполнять двойную функцию: сокращение электрической длины спиральной структуры, и сдерживание высоковольтных разрядов пока напряжение не вырастет до желаемого потенциала. Очевидно, также следует, что когда измеряется распределение напряжение по структуре под электродом, итоговое напряжение будет суперпозицией картины стоячих волн в передающей линии плюс обратный r потенциал верхнего электрода.) При помощи обычной теории распределенных элементов, сложная краевая задача была сведена к очень простому случаю передающей линии. Фактически, очень удобно весь расчет и настройку системы (см. рисунок 2) выполнять по диаграмме Смита (Вольперта-Смита).^27,28

 

IV. НАСТРОЙКА РАСПРЕДЕЛЕННЫХ СИСТЕМ

 

Теперь мы переходим к настройке ансамбля винтовых резонаторов. Из уравнения (54), распределение напряжения вдоль четвертьволновой структуры можно аппроксимировать (см. Failure_of_Classic_Theory.htm )

 

 

 

где координата х измеряется обратно от нагрузки, как показано на рис. 2. Суперпозиция прямых и обратных бегущих волн образует пространственную систему стоячих волн распределения напряжения вдоль резонатора. Причем нулевое напряжение в базе (x = - h), максимальное напряжение в верхней части (x = 0) и синусоидальная зависимость вдоль структуры. Представляет интерес изучить поведение системы при фиксированной рабочей частоте. При сокращении электрической длины винтового волновода с 90° до 15°, емкость резонансного конденсатора должна увеличиваться (см. Рис 3.) Кроме того, напряжения спадает от вершины синусоиды (фаза 90°) к линейной части синусоиды (при высотах катушки, где фаза менее 15°). При таких коротких высотах, можно использовать только первый член в разложении Тейлора для выражения (54) в точке x = - h, и рост напряжения подобен тому, какой был бы для вторичной обмотки трансформатора при равномерном распределении тока (случай обычного трансформатора). В таких условиях, система переходит к классическому режиму сосредоточенных элементов, и теряется преимущество режима с высоким значением S_КСВН (коэффициента стоячей волны по напряжению), открытого Тесла.

 

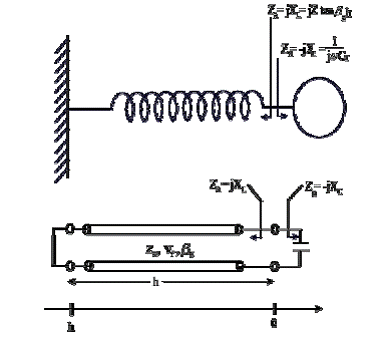
Рисунок 2. Распределенный резонатор, с емкостью подстройки

 

V. ПЕРЕХОД К КЛАССИЧЕСКОЙ ТЕОРИИ ЦЕПЕЙ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ

 

A. Классические индуктивности.

 

Классическая теория цепей для сосредоточенных элементов подразумевает, что не существует явления волновой интерференции, то есть – ток на входных и выходных контактах элементов цепи одинаковый. Это утверждение базируется  на двух предпосылках:

1. Пространственной однородности функции распределения тока по каждому элементу.

2. Пространственная задержка фазы между входом и выходом схемы равна нулю.

Эффект сдвига фаз (пункт 2) происходит двумя путями:

во-первых, потому что скорость света с в действительности не бесконечна, и эффект начинает проявляться, когда время для пространственного распространения сигнала из одной части схемы в другую, становится заметным по сравнению со временем периода колебаний тока;

во-вторых, когда время, необходимое для распространения сигнала по проводникам схемы,  становится заметным по сравнению со временем периода колебаний тока.

Ramo и Whinnery отметили, что пункт 1 тесно связано с пунктом 2, и прокомментировали “если в данный момент, ток изменяется вдоль пути следования... должно появиться накопление, или рассредоточение заряда в различных точках контура”²⁹. Распределение тока в таких условиях будет пространственно неоднородно. (Уравнение неразрывности все еще выполняется, конечно.) Профессор King утверждал: “Вся классическая теория цепей для сосредоточенных элементов основана на [этих] двух предположениях ... и настолько, что она редко считает необходимым даже упоминать о существовании таких ограничений на общность теории.”³⁰ Все дело в том, что про эти ограничения часто забывают. Кроме того, все стандартные формулы для индуктивностей в справочниках основаны на этих двух предположениях. Чтобы убедиться в этом, рассмотрим, как была получена стандартная формула для “индуктивности”. Интеграл поля и соответственно поток, в действительности, являются функциями от распределения тока. Но, в предположении, что ток пространственно однороден (I(ľ) = I₀ ), его можно вынести из-под знака интеграла, так что магнитный поток на единицу тока будет определяться чисто геометрической формулой Неймана³¹

 

 

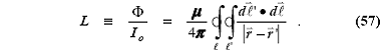
Именно эта процедура (которая не учитывает различий в пространственном распределении тока в катушках), используется в справочниках при выводе формул для собственной и взаимной индуктивности. Конечно, предположение о равномерном распределении тока, не применимо для катушек, работающих вблизи собственного резонанса! Sichak вывел выражение для волнового сопротивления катушки и постоянной распространения, основываясь на следующем утверждение, “Стандартная формула для индуктивности длинного соленоида может быть получена, если рассматривать соленоид, как короткозамкнутую винтовую передающую линию с короткой длиной, и используя уравнение (43) для волнового сопротивления Z_c и уравнения (28) для постоянной распространения”³². То есть, так как tan(x) » x для малых x, импеданс короткой линии на выходе становится

 

 

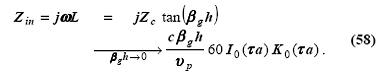
Согласно Sichak, это соотношение сводится к классической формуле индуктивности для сосредоточенных элементов.

 

 

 

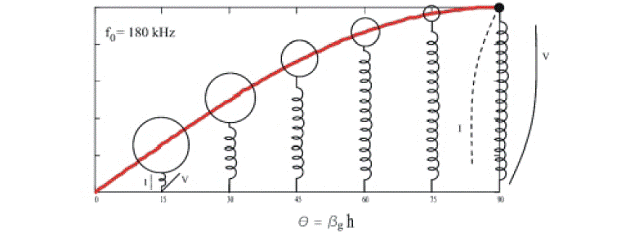
Рисунок 3. Сплошная красная кривая показывает рост напряжения вдоль четвертьволнового резонатора и линейный участок перехода к классической теории сосредоточенных элементов. По мере увеличения емкости нагрузки (при постоянной резонансной частоте), высота передающей линии должна сокращаться … пока она не станет вести себя как классическая индуктивность с равномерным распределением тока и линейным ростом напряжения

 

B. А что с вопросом собственной емкости?

 

Поведение распределенных сетей (например, проводов, периодических физических структур, спиралей, гофрированных волноводов, антенн и т.д.) может быть удобно представлено парой терминалов из классических сосредоточенных элементов. Paris и Hurd говорили: “Это обычная практика говорить о кочующих или распределенных эффектах, когда поведение схемы или устройства, не может быть предсказано на основе обычной классической теории сетей.”³³ Несостоятельность любой теории цепей  сосредоточенных элементов в описании реального мира, лежит в предпосылке, заложенной в их основе: скорость света предполагается бесконечной в волновом уравнении (мгновенная скорость передачи сигнала в любую точку пространства³⁴). Следовательно, классическая теория цепей сосредоточенных элементов не в состоянии (и не может) точно интерпретировать мир дифференциальных уравнений частных производных второго порядка в пространстве и времени. Классические сосредоточенные элементы “не имеют физических размеров и предпочтительной ориентации в пространстве; их можно перемещать и вращать по своему усмотрению.”³⁵. Это не так для реальных катушек.

Что такое собственная емкость катушки? Физический подход состоит в рассмотрении каждого витка катушки как  конденсатора, а вне границ катушки, как расширяющийся набор емкостей, уходящий в окружающее пространство. Этот вопрос связан с физическим пониманием того факта, что реактивность катушки это ни то, что дают формулы расчета индуктивности из справочников (для равномерного распределения тока), и ни то, что получается путем измерения L на частоте 1 кГц и умножения на частоту ω.

 Концепция “собственной” емкости катушки состоит в попытке обойти последствия эффектов передающей линии для маленьких катушек, когда распределение тока перестает быть постоянным. Типичным подходом к решению такой задачи является следующая процедура: стартуют с уравнений Максвелла и используют только первые два слагаемых из разложения в ряд Тейлора для распределенного тока, и в итоге получается выражение собственного импеданса для обобщенной закрытой цепи.³⁶ После раскрытия интеграла Неймана для собственной индуктивности, оставшийся отрицательный компонент реактивности позволяет получить выражение для собственной емкости катушки. Эти формулы справедливы для параллельного контура из  индуктивности и емкости, при рабочей частоте намного ниже 1/ Ö LC_L. Они позволяют рассматривать катушку со слегка неоднородным распределением тока, как будто бы ток равномерен и катушка зашунтирована классической емкостью. Существует большой ряд формул для собственной емкости катушки.^37,38  Ни одна из них, не представляет никакой ценности для четвертьволновых винтовых резонаторов в окрестности 90° точки. Они имеют определенный смысл только для катушек“из большого количества витков тонкой проволокой”, если они работают значительно ниже их собственного резонанса, но эти “индукционные катушки”; не являются настоящими катушками Тесла. Применение “большого количества витков тонкой проволокой” для построения катушки Тесла, обречено на провал. Тесла, по сути, отказался от такой практики уже в 1893 году. (К 1897 году он использует “прочный кабель № 8”.)

Прим. переводчика:

№ 6 → 1/6 дюйма → диаметра жилы » 4 мм

№ 8 → 1/8 дюйма → диаметра жилы » 3 мм

№ 10 → 1/10 дюйма → диаметра жилы » 2.5 мм

№ 18 → 1/18 дюйма → диаметра жилы » 1 мм

 

Medhurst попытался описать катушку с заземленной базой и с неоднородным током (т. е. катушку с пространственными модами), как классическую сосредоточенную индуктивность (с известной формулой индуктивности для низкой частоты) и включенным параллельно с ней паразитным сосредоточенным конденсатором, значение емкости которого получено эмпирически, но не физически. Построив много катушек, проведя измерения их резонансных частот и индуктивностей на низких частотах (где распределение I(z) является равномерным - что, конечно, на резонансной частоте совсем не так), ему удалось получить набор синусоидальных стационарных кривых для  “собственной емкости ”. По ним он вывел зависимость емкости от такого параметра, как отношение длины катушки к диаметру. Эмпирически полученная “собственная емкость” хорошо описывается кривой

 

 

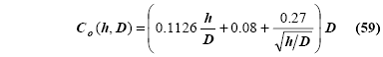
где C_o (в пикофарадах), h осевая длина (или высота) катушки и D диаметр катушки (в см). Конечно, это просто статистическое решение, пригодное для вычислений в конкретном h/D режиме, а вовсе не физическая величина. Это чисто эмпирическое определение, характеризующее импеданс структуры в виде пары терминалов. Ведь задача состояла в том, чтобы представить настоящую катушку (которая имеет неоднородное распределение тока), как классическую индуктивность (в ней предполагается равномерное распределение тока) и параллельного ей, нефизической эффективной емкости. Формула не дает (и, оставаясь формулой для сосредоточенных элементов, не может дать) выражение для увеличения напряжения, из-за имеющихся в реальности стоячих волн тока в винтовой структуре, но она позволяет представить реактивность резонатора, в виде терминальной модели.

 

 

 

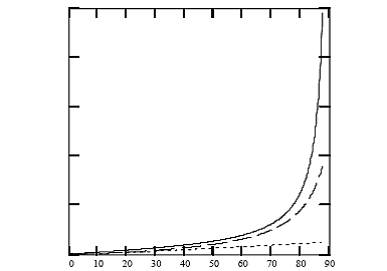
Рисунок 4. График индуктивной реактивности в зависимости от электрической длины катушки в градусах: реальная (сплошная линия), эмпирическая формула Medhurst  с паразитной емкостью (пунктир), и классическая формула (пунктир).

 

Такую же (или даже лучше) формулу можно было бы получить из решения уравнений поля, с помощью проведения “численного эксперимента” с уравнениями (43) и (53). На рисунке 4 сравниваются графики реактивности катушки для точного решения уравнения поля, аппроксимация Medhurst, и формулы для классической индуктивности, в зависимости от ее осевой длины. Если интересует только импеданс катушки, то эмпирическая аппроксимация Medhurst приемлема примерно до 60°.

 

VI. ОБСУЖДЕНИЕ

 

A. Эксплуатационные характеристики

 

Некоторые утверждают, что производительность катушки Тесла определяется отношением длины разряда к высоте катушки Тесла. Как видно из рисунка 3, это заблуждение. Если следовать этому критерию, (поскольку электрический пробой обратно пропорционален кривизне электрода – чем больше шар, тем меньше кривизна и соответственно выше потенциал пробоя) можно было бы сделать очень короткую катушку с огромным верхним электродом, - и очень большим потенциалом пробоя. Ошибка в том, что такая короткая катушка будет работать в классическом режиме сосредоточенной индуктивности (равномерное распределение тока) и рост напряжения ограничен максимальным значением из выражения для связанных контуров,

 

 

которое подразумевает не только классический режим для сосредоточенных элементов, но и также полную передачу энергии во вторичку (при правильных длительностях переключения), и отсутствие потерь в системе. С этой ошибочной философией, потребуется гораздо большее количество энергии, чтобы достичь такого потенциала пробоя, который может дать относительно простой распределенной резонатор, работающий в режиме стоячей волны. Тесла, комментируя это заблуждение, касающееся винтовых катушечных резонаторов, говорил, “Большая емкость в сочетании с маленькой индуктивностью - это наихудший вариант цепи, который может быть построен. ”³⁹ Сейчас всем должно быть ясно, почему Тесла был прав, и это истина. Потенциал пробоя определяется размерами электрода. Так как, рост напряжения пропорционален 1/ah (подлинный параметр производительности резонатора), тот же потенциал может быть достигнут с гораздо меньшей затратой энергии с помощью стоячих волн в системе, например, как в случае с резонатором электрической высотой в 75°, и резонатором, работающем в классическом режиме сосредоточенной индуктивности высотой всего лишь в 10°. Хотя мы знаем, что природа не имеет дела с бесконечными величинами, теперь мы можем понять, почему Тесла говорил: “С такими катушками, я обнаружил, что практически не существует предела достижимой напряженности”⁴⁰ и по другому поводу: “Я получал электрические разряды длиной более чем в 100 футов; но не составит труда достичь длины в сто раз большей.”⁴¹  Если уравнение (60) жестко ограничено, то уравнение (55) дает фундаментальный предел, к которому необходимо стремиться при наращивании напряжения. Практически все высокопроизводительные катушки Тесла, это распределенные волноводные резонаторы медленной волны. Кстати, Тесла сказал, что он открыл это замечательное свойство высокочастотных катушек в 1894, "Это был первый шаг к… моему усиливающему передатчику». ⁴²  Интересно отметить, что приведенный выше анализ также имеет место, когда винтовая катушка сводится к случаю линейного проводника. Примером этому могут служить четвертьволновые коаксиальные резонаторные передающие линии (катушки Тесла в несбалансированном “монопольном режиме”) и спаренные параллельные резонаторные линии передачи (катушки Тесла в сбалансированном “дипольном режиме”).

 

B. Фундаментальные ограничения

 

Необходимость расширения настоящего анализа на квазимонохроматические, частично-когерентные волновые распределения, должна быть очевидной. Ключевым параметром производительности высоковольтных катушек Тесла является S_КСВН (коэффициент стоячей волны по напряжению) самой резонансной структуры - чем выше, тем лучше! И зависит от способности прямой и обратной волны конструктивно интерферировать, это аналогично такому понятию в оптике, как «гребенка» (или фильтр) оптической  прозрачности (пропускания) среды для квазимонохроматических, частично когерентных лучей.⁴³ Фактически, настоящая катушка Тесла является волноводным аналогом с медленными волнами, резонатору/интерферометру Фабри-Перо с проводящей поверхностью на одной плоскости и высоким сопротивлением на другой. Возбуждая катушку Тесла LC-разрядами, можно получить настолько плохо спроектированный резонатор (как в философии “большого количества витков тонкой проволокой”), что прямые и обратные волны будут так нескоррелированны, что распределение напряжения получится практически равномерным - нет ни минимумов, ни максимумов вдоль структуры!

 

C. Другие модели винтовых катушек

 

В дополнение к волновому сопротивлению винтовой катушки, рассмотренному выше, существует множество выражений для волнового сопротивления, которые были разработаны в приложениях волноводов бегущей волны. Они представляют определенный интерес, и даже применимы к модели винтовой катушки.⁴⁴ Кроме того, вышеприведенный анализ был основан на модели спиральной поверхности Ollendorf, которая представляет винтовую катушку, как анизотропно проводимую поверхность. Существуют и другие модели винтовых катушек. «Тонкопроволочная» модель Kogan может быть получена либо из уравнения электрического вектора Герца, или из уравнения векторного потенциала.^{45, 46} Bondar также изучал тонкопроволочную модель.⁴⁷ Модель спиральной ленты Sensiper⁴⁸ выявляет много интересных периодических свойств у волн, распространяющихся по спирали. Очень жаль, что в настоящей статье мы не нашли места представить экспериментальные измерения. Статья с этими данными была подготовлена для экспериментаторов с катушкой Тесла, и напечатана несколько лет назад в литературе для радиолюбителей.⁴⁹

 

D. Негармонические сигналы

 

Мы отмечаем, что вышеприведенные рассуждения (в том числе работа Medhurst), лежат в рамках синусоидального стационарного состояния. Многие экспериментаторы возбуждают свои катушки переходными формами сигнала, которые, по сути, являются сигналами с конечной энергией, в то время как периодические волны являются сигналами конечной мощности. Концептуально (и практически)  импульсный (с конечной энергией) широкополосный отклик системы можно определить, используя идею синтезированного импульса, получаемого из разложения в спектр Фурье переходной формы сигнала возбуждения. Определяется ответ системы на каждый отдельный спектральный компонент, а затем комбинируется для получения результата.⁵⁰ Это особенно легко сделать для высокодобротных резонаторов, поскольку время когерентности волн в структуре достаточно большое. Канонические переменные, по существу, являются адиабатическими инвариантами.

 

VII. ВЫВОДЫ

 

В настоящей статье высокочастотные катушки моделируются, как анизотропные  волноводы с медленными волнами. Решение краевой задачи дало не только определение полей, но и уравнение с собственными значениями для параметра распространения (τ), коэффициент замедления скорости (V_f), эффективное волновое сопротивление (Z_c), а также предельное значение роста напряжения (1/ah), благодаря  волновой интерференции пространственных мод волновода. Эти параметры позволяют провести подробный инженерный анализ винтовой катушки, представленной в виде простой модели поверхностной передающей линии, и их можно применить для проектирования и настройки винтового резонатора (катушки Тесла), с помощью обычной диаграммы Смита (Вольперта-Смита). Кроме того, этот подход позволяет квалифицированно провести концептуально плавный переход от теории поля ® к распределенным элементам ® к сосредоточенным элементам.

 

БЛАГОДАРНОСТИ

 

Авторы хотели бы выразить признательность г-ну Scott Kapin за подготовку рисунков и г-ну Basil Pinzone за техническую поддержку.

 

ССЫЛКИ

 

¹ The quote is taken from Tesla’s lectures before the Institution of Electrical Engineers (London) and the Royal Institution (London),February 3 and 4, 1892, published in the Journal of the IEE(London), Vol. XXI, 1892, p. 51. Reprinted in Experiments with Alternate Currents of High Potential and High Frequency, by Nikola Tesla, McGraw-Hill, 1904, p. 6. [From “Obituary,”Electrical Engineering, Vol. 62, January, 1943, p. 76, we see that he was elected a Fellow of the AIEE in 1917, and that he served as AIEE Vice-President from 1892-1894.]

² R. Adler, L.J. Chu, and R. Fano, Electromagnetic EnergyTransmission and Radiation, Wiley, 1960, p. 202.

³ J.R. Pierce, “Theory of the Beam-Type Traveling-Wave Tube, ”Proceedings of the IRE, 1947, pp. 111-123. (See Appendix B, “Propagation of a Wave Along a Helix”.)

⁴ F. Ollendorf, Die Grundlagen der Hochfrequenztechnik, Springer, Berlin, 1926, pp. 79-87.

⁵ R.E. Collin, Foundations for Microwave Engineering, McGraw-Hill, 1966, pp. 392-398, 476-482.

⁶ P. Vizmuller, Filters with Helical and Folded Helical Resonators, Artech House, 1987, pp. 77-85.

⁷ J.D.Kraus, Antennas, McGraw-Hill, 2nd ed., 1988, p. 274.

⁸ R.E. Collin, Foundations for Microwave Engineering, McGraw-Hill, 1966, pp. 392-398.

⁹ N. Contaxes and A.J. Hatch, “High-Frequency Solenoidal Coils,”Jour. Appl. Phys., Vol. 40, 1969, pp. 3548-3550.

¹⁰ R. Fano, L.J. Chu, and R.B. Adler, Electromagnetic Fields, Energy and Forces, Wiley, 1960, pp. 257 -259.

¹¹ R. Rudenberg, “Electromagnetic Waves in Transformer CoilsTreated by Maxwell's Equations,” Jour. Applied Physics, Vol. 12,1941, pp. 219-229. See Fig. 6.

¹² D. Watkins, Topics in Electromag. Theory, Wiley, 1958, p. 44.

¹³ H.C. Pocklington, “Electrical Oscillations in Wires,” Proc.Cambridge Philosophical Society, Vol. 9, 1897, pp. 324-332.

¹⁴ A.G. Kandoian, and W. Sichak, “Wide Frequency Range Tuned Helical Antennas and Circuits,” Electrical Communications, Vol.30, 1953, pp. 294-299.

¹⁵ J.R. Pierce, 1947, loc cit.

¹⁶ W. Sichak, “Coaxial Line with Helical Inner Conductor,”Proceedings of the IRE, 1954, pp. 1315-1319. (Corrections,February, 1955, p. 148.)

¹⁷ G.N. Watson, A Treatise on the Theory of Bessel Functions,Cambridge University Press, 2nd edition, 1944, pp. 79-80.

¹⁸ H.B. Dwight, Table of Integrals, 4th ed., 1961, pp. 195, 197.

¹⁹ F.E. Terman, “Resonant Lines in Radio Circuits,” Electrical Engineering, July, 1934, pp. 1046-1053.

²⁰ D.H. Sloan, “A Radio frequency High-Voltage Generator,”Physical Review, Vol. 47, 1935, pp. 62-71.

²¹ E.U. Condon, “Forced Oscillations,” Journal of Applied Physics,Vol. 12, 1941, pp. 129-132.

²² R.I. Sarbacher and W.A. Edson, Hyper and Ultra-High Frequency Engineering, Wiley, 1943, pp. 351-353.

²³ J.D. Ryder, Networks, Lines and Fields, Prentice-Hall, 2ndedition, 1955, p. 348.

²⁴ E.C. Jordan and K.G. Balmain, Electromagnetic Waves and Radiating Sys., Prentice-Hall, 2nd edition, 1968, pp. 226-231.

²⁵ E.A. Abramyan, Indust. Electron Accelerators and Applications, Hemisphere Publishing Co., 1988, pp. 88-89. (See Fig. 6.4b.)

²⁶ W. Heise, “Tesla Transformatoren,” ElektroTechnicheZeitschrift, Vol. 85, 1964, pp. 1-8.

²⁷ J.F. Corum and K.L. Corum, “A Technical Analysis of the Extra Coil as a Slow Wave Helical Resonator,” Proc. 1986 Intl. TeslaSymp., Colorado Springs, CO, 1986, Chapt. 2, pp. 1-24.

²⁸ J.F. Corum and K.L. Corum, “The Application of Transmission Line Resonators to High Voltage RF Power Processing: History,Analysis and Experiment, Proceedings of the 19th SoutheasternSymposium on System Theory, March, 1987, pp. 45-49.

²⁹ S. Ramo and J.R. Whinnery, Fields and Waves in Modern Radio, Wiley, 2nd ed., 1953, pp. 222-223.

³⁰ R.W.P. King, Electromagnetic Engineering, McGraw-Hill, 1945,(reprinted by Dover in 1963 as Fundamental ElectromagneticTheory), p. 421.

³¹ F. Neumann, “Die mathematischen Gesetze der inducirtenelektrischen Strome,” Berl. Akad. der Wiss., Abh. 1845.

³² 1W. Sichak, loc cit.

³³ D.T. Paris and F.K. Hurd, Basic Electromagnetic Theory,McGraw-Hill, 1969, p. 527.

³⁴ J.D. Jackson, Classical Electrodynamics, 2nd edition, Wiley,1975, pp. 598-600.

³⁵ R.E. Scott, Linear Circuits, Addison-Wesley, 1960, p. 4.

³⁶ R.W.P. King, Electromagnetic Engineering, McGraw-Hill, 1945,(reprinted by Dover in 1963 as Fundamental Electromagnetic Theory), Chapter VI.

³⁷ See, for example: “On the Effect of Distributed Capacity in Single Layer Coils,” by J.C. Hubbard, Phys. Rev., Vol. 9, 1917,p. 529; “Distributed Capacity and Its Effect,” by S. Cohen, The Electrical Experimenter, May, 1917, pp. 33, 65; “The Effective Self-Capacity, Inductance and Resistance of Coils,” by G.W.O.Howe, Jour. IEE (London), Vol. 60, 1922, pp. 67-72.;“Distributed Capacity of Single Layer Coils,” by A.J. Palermo,Proc. I.R.E., Vol. 22, 1934, p. 897.

³⁸ R.G. Medhurst, “H.F. Resistance and Self-Capacitance of Single-Layer Solenoids,” Wireless Engr., Pt. 1 - February, 1947, pp. 35-43; Pt. 2 - March, 1947, pp. 80-92. (pp. 84, 86.)

³⁹ L.I. Anderson, Tesla on His Work with Alternating Currents, SunPublishing Co., 1992, p. 74.

⁴⁰ N. Tesla, “Some Experiments in Tesla’s Laboratory with Currentsof High Potential and High Frequency,” Electrical Review (NY),March 29, 1899, pp. 195-197, 204.

⁴¹ N. Tesla, “The Problem of Increasing Human Energy,” CenturyIllustrated Magazine, June 1900, pp. 175-211.

⁴² L.I. Anderson , loc cit, p. 72.

⁴³ M. Born and E. Wolf, Principles of Optics, 5th edition, PergamonPress, 1975, p. 506.

⁴⁴ J.A. Mezak, “Modeling Helical Air Coils for Wireless and RFApplications,” RF Design, January, 1998, pp. 77-79.

⁴⁵ K.H. Kogan, Soviet Phys. Doklady, Vol. 66, 1949, pp. 867-870.

⁴⁶ K.H. Kogan, Soviet Phys. Doklady, Vol. 107, 1956, pp. 541-544.

⁴⁷ V.M Bondar, “Propagation of an Electromagnetic Wave along a Filamentary Helix,” Radiotekhnika, No. 11, 1985, pp. 82-84.

⁴⁸ S. Sensiper, “Electromagnetic Wave Propagation on HelicalStructures,” Proc. of the IRE, February, 1955, pp. 149-161.

⁴⁹ K.L. Corum and J.F. Corum, “Tesla Coils and the Failure of Lumped-Element Circuit Theory,” TCBA News, Vol. 18, No. 3,July/August/September, 1999, pp. 13-18.50 L.A. Robinson, W.B. Weir and L. Young, “An RF Time-Domain Reflectometer Not in Real Time,” IEEE Transactions MicrowaveTheory, Vol. MTT-20, 1972, pp. 855-857.

 

 

Послесловие к переводу

 

·         [для экспериментаторов, использующих качер в качестве источника раскачки катушки Тесла] –

 

Манипуляции вблизи катушки, разрушают сложившуюся картину стоячих волн и могут привести к высоковольтному выбросу со стороны нижнего выхода катушки, подключенного к базе/затвору транзистора. Превышение предельно допустимого режима по напряжению при таком выплеске – основная причина выхода из строя транзисторов.